程序语言数据结构
,

稀疏矩阵和广义表

Catalogue   
  1. 1. 定义
    1. 1.1. 矩阵
    2. 1.2. 稀疏矩阵的存储结构
      1. 1.2.1. 顺序存储
      2. 1.2.2. 链式存储
    3. 1.3. 广义表(Generalized List)
      1. 1.3.1. 抽象数据类型
      2. 1.3.2. 存储
        1. 1.3.2.1. 头尾链表存储结构
        2. 1.3.2.2. 扩展线性链表存储结构
  2. 2. 参考

定义

矩阵

矩阵是一个具有m行 x n列的数表，共包含m x n个数（元素），每个元素处在确定行和列的交点位置上，都与一对行号和列号唯一对应。
当一个矩阵中的行数和列数相同时，即m = n时则称为n阶矩阵或方阵。

稀疏矩阵（SparseMatrix）是矩阵中的一种特殊情况，其非零元素的个数小于零元素的个数。

对于稀疏矩阵中的每个非零元素，可用它所在的行号、列号以及元素这三元组（i，j，aij）来表示。若把所有的三元组按照行号为主序（即主关键字）、
列号为辅序（次关键字）进行排序，就构成一个表示稀疏矩阵的三元组线性表。

((1,1,3),(1,4,5),(2,3,-2),(3,1,1),(3,3,4),(3,5,6),(5,3,-1))

稀疏矩阵的存储结构

顺序存储

链式存储

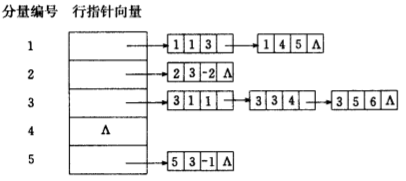
  1. 带行指针向量的链接存储

    在这种链接存储中，需要把具有相同行号的三元组结点按照列号从小到大的顺序链接成一个单链表，每个三元组结点的类型可定义为：

1
2
3
4
5
6
7
class TripleNode:

    def __init__(self):
        self.row = 0
        self.col = 0
        self.val = None
        self.next = None  # 指向同一行的下一个结点

稀疏矩阵中的每一行对应一个单链表，每一个单链表都有一个表头指针，为了把它们保存起来，便于访问每一个单链表，需要一个行指针向量，该向量中的第i
个分量用来存储稀疏矩阵中的第i行所对应的单链表的表头指针。

1
2
3
4
5
6
7
8

class LMatrix:

    def __init__(self):
        self.m = 0
        self.n = 0
        self.t = 0  # 非零元素的个数
        self.vector = []

  1. 十字链接存储

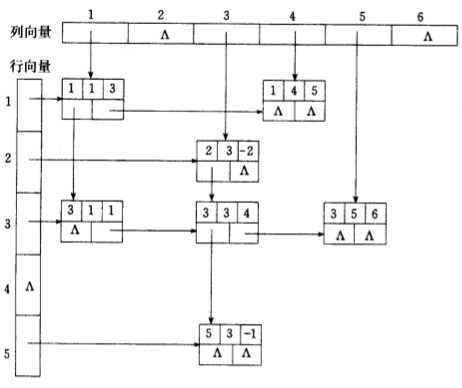
既带行指针向量又带列指针向量的链接存储。在这种链接存储中，每个三元组结点既处于同一行的单链表中，又处于同一列的单链表中，即处于所在的行单链表
和列单链表的交点处。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class CrossNode:

    def __init__(self):
        self.row = 0
        self.col = 0
        self.val = None
        self.right = None  # 存储指向同一行下一个结点的指针
        self.down = None  # 存储同一列下一个结点的指针

class CLMatrix:

    def __init__(self):
        self.m = 0
        self.n = 0
        self.t = 0
        self.rv = []  # 行向量指针，存储行单链表的表头指针
        self.cv = []  # 列向量指针，存储列单链表的表头指针


广义表(Generalized List)

一个广义表是n（n ≥ 0）个元素的一个序列，当n = 0时则称为空表。在一个非空的广义表中，其元素可以是某一确定类型的对象（这种元素被称为单元素），
也可以是由单元素构成的表（这种元素可相对的被称为子表或表元素）。显然，广义表的定义是递归的。

设ai为广义表的第i个元素，则广义表的一般表示与线性表相同：

(a1,a2,a3,…,ai,…,an)

其中n表示广义表的长度，即广义表中所含元素的个数，n ≥ 0。

深度：表中括号的最大层数

表示方式

用小写字母表示单元素，用大写字母表示表

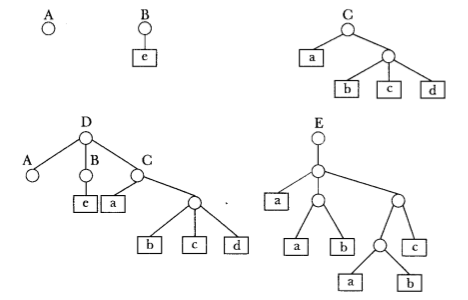
A = ()
A是空表，长度为0，深度为1。

B = (e)
B是长度为1的广义表，深度为1。线性表。

C = (a, (b,c,d))
C是长度为2的广义表，深度为2。

D = (A, B, C) = ((), (e), (a, (b, c, d)))
D是长度为3的广义表，深度为3。A、B、C为子表。

E = ((a, (a,b), ((a,b), c)))

用圆圈和方框分别表示表和单元素，并用线段把表和它的元素连接起来，则可得到一个广义表的图形表示。

抽象数据类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
ADT GList{

数据对象： D={ei | i=1,2,...,n; n>0; ei∈AtomSet 或ei∈GList,
          AtomSet为某个数据对象 }

数据关系： R1={<ei-1,ei> | ei-1,ei∈D, 2<=i<=n}

基本操作：

	InitGList(&L);
	  操作结果： 创建空的广义表L。

	CreateGList(&L, S);
	  初始条件： S是广义表的书写形式串。
	  操作结果： 由S创建广义表L。

	DestroyGList(&L);
	  初始条件： 广义表L存在	
	  操作结果： 销毁广义表L。

	CopyGList(&T, L);
	  初始条件： 广义表L存在
	  操作结果： 由广义表L复制得到广义表T。

	GListLength(L);
	  初始条件： 广义表L存在
	  操作结果： 求广义表L的长度

	GListenDepth(L);
	  初始条件： 广义表L存在
	  操作结果： 求广义表L的深度

	GListEmpty(L);
	  初始条件： 广义表L存在
	  操作结果： 判定广义表L是否为空

	GetHead(L);
	  初始条件： 广义表L存在
	  操作结果： 取广义表L的头

	GetTail(L);
	  初始条件： 广义表L存在
	  操作结果： 取广义表L的尾

	InsertFirst_GL(&L, e);
	  初始条件： 广义表L存在
	  操作结果： 插入元素e作为广义表L的第一元素

	DeleteFirst_GL(&L, &e);
	  初始条件： 广义表L存在
	  操作结果： 删除广义表L的第一元素，并用e返回其值

	Traverse_GL(L, Visit());
	  初始条件： 广义表L存在
	  操作结果： 遍历广义表L，用函数Visit处理每个元素
}ADT GList;

存储

在一个广义表中，其数据元素有单元素和子表之分，所以在对应的存储结构中，其存储结点也有单元素结点和子表结点之分。对于单元素结点，应包括值域
和指向其后继结点的指针域；对于子表结点，应包括指向子表中第一个结点的表头指针域和指向其后继结点的指针域。为了把广义表中的单元素结点和子表
结点区别开，还必须在每个结点中增设一个标志域，让标志域取不同的值，从而区别不同的结点。

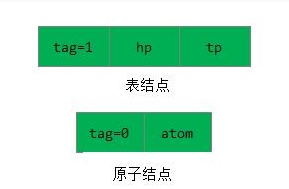
由于列表中的数据元素可能为原子或列表， 由此需要两种结构的结点： 一种是表结点，用于表示列表；一种是原子结点，用以表示原子。若列表不空，则可分解成表头和表尾；反之，一对确定的表头和表尾可唯一确定列表。由此，一个表结点可由3个域组成： 标志域、指示表头的指针域和指示表尾的指针域； 而原子结点只需两个域： 标志域和值域。

头尾链表存储结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//------ 广义表的头尾链表存储表示 -------

typedef enum{
	ATOM,          //ATOM == 0: 原子
	LIST           //LIST == 1: 子表
}ElemTag;

typedef GLNode{
	ElemTag tag;                     //公共部分，用于区分原子结点和表结点
	
	union{                           //原子结点和表结点的联合部分
		AtomType atom;               //atom是原子结点的值域，AtomType由用户定义
		struct{
			struct GLNode *hp;
			struct GLNode *tp;
		}ptr;                        //ptr是表节点的指针域，ptr.hp和ptr.tp分别指向表头和表尾
	}
}*GList;                             //广义表类型
扩展线性链表存储结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//------ 广义表的扩展线性链表存储表示 -------

typedef enum{
	ATOM,          //ATOM == 0: 原子
	LIST           //LIST == 1: 子表
}ElemTag;

typedef GLNode{
	ElemTag tag;                     //公共部分，用于区分原子结点和表结点
	
	union{                           //原子结点和表结点的联合部分
		AtomType atom;               //atom是原子结点的值域，AtomType由用户定义
		
		struct GLNode *hp;           //表结点的表头指针
	};
	
	struct GLNode *tp;               //相当于线性链表的next，指向下一个元素结点
}*GList;

参考

SciPy使用多个数据结构为创建稀疏矩阵提供了工具，以及将稠密矩阵转化为稀疏矩阵的工具。

  • csc_matrix: Compressed Sparse Column format
  • csr_matrix: Compressed Sparse Row format
  • bsr_matrix: Block Sparse Row format
  • lil_matrix: List of Lists format
  • dok_matrix: Dictionary of Keys format
  • coo_matrix: COOrdinate format (aka IJV, triplet format)
  • dia_matrix: DIAgonal format